There are two types of heap. First one is Max heap and second one is min
heap. Max heap is a special type of binary tree .The roots of the max heap
is greater than its child roots. Other heap is min heap it is also a special
type of heap which has minimum root than his child. We can sort the array values
using heap sorting algorithm. In this algorithm the heap build is used to
rebuild the heap.
In this example we sorting all elements of an array. The complexity of the heap sort is O(n.log(n)). Heap sort is slowest but it is better option for large data sets.
To sort a heap Build Heap algorithm is used to build a heap out of the data set
Algorithm: Add the elements to a heap one at a time. Then remove the elements from the top of the heap one at a time, and they will be in order. If the heap is done upside down (i.e. largest element at the root) then the incomplete sorted list and the heap can share the same array without requiring extra memory.
Steps of heap sort algorithm:
1. Remove the parent root and replace it with the rightmost leaf.
2.Store parent root in an array.
3. Re-establish the heap.
4. Repeat steps 1 and 3 until values in heap is not zero.
Pros:
Working of heap sort algorithm:
Input:1,3,5,4,2
Step1:Buid Heap tree and an array of same size.

Step2: Remove largest root and add largest root in array.

Step3:Replace last value (eg 2) at at root node position.

Step4:Swap 2 and 4

Step5:Swap 2 and 3.
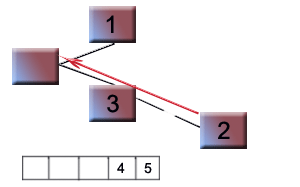
Step6:Remove 4 and replace 2 at position of 4 and add 4 in array
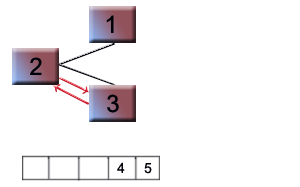
Step7:Swap 2 and 3

Step8:Remove 3 ,add in array and replace 1 at position of 3.

Step9:Swap 2 and 1.
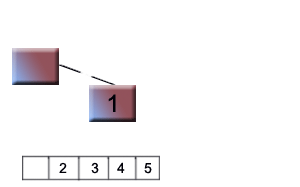
Step10:Remove 2 and it at root position

Step11:Remove 1 and add in array.
Output: Sorted array 1,2,3,4,5
Notes: This isn't an especially useful sort, but the running time is guaranteed O(n.log n) and it is very light on memory consumption. Also, if you have already implemented a heap for some other reason, then this sort comes almost for free. It is possible to get some extra speed by constructing the heap in one pass: put everything into the heap ignoring the heap condition, then work through the heap from bottom to top, bubbling elements down the heap where necessary. This makes the heap creation take linear time.
In this example we sorting all elements of an array. The complexity of the heap sort is O(n.log(n)). Heap sort is slowest but it is better option for large data sets.
To sort a heap Build Heap algorithm is used to build a heap out of the data set
. Then remove the root element and replace the last element at the
position of root node. Then rearrange the heap. Place the root node in an array.
Follow these steps until all elements in heap is not replace into array. The
values in array will be in sorted order.Algorithm: Add the elements to a heap one at a time. Then remove the elements from the top of the heap one at a time, and they will be in order. If the heap is done upside down (i.e. largest element at the root) then the incomplete sorted list and the heap can share the same array without requiring extra memory.
Steps of heap sort algorithm:
1. Remove the parent root and replace it with the rightmost leaf.
2.Store parent root in an array.
3. Re-establish the heap.
4. Repeat steps 1 and 3 until values in heap is not zero.
Pros:
- Guaranteed to be O(n.log n)
- One of the few non-recursive O(n.log n) sorts
- Fairly easy to debug, because it is non-recursive and because it consists of two smaller and unrelated parts
- Not as fast on average as Quick sort
- Quite a lot of code to implement the heap operations.
Working of heap sort algorithm:
Input:1,3,5,4,2
Step1:Buid Heap tree and an array of same size.

Step2: Remove largest root and add largest root in array.

Step3:Replace last value (eg 2) at at root node position.

Step4:Swap 2 and 4

Step5:Swap 2 and 3.

Step6:Remove 4 and replace 2 at position of 4 and add 4 in array

Step7:Swap 2 and 3

Step8:Remove 3 ,add in array and replace 1 at position of 3.

Step9:Swap 2 and 1.

Step10:Remove 2 and it at root position

Step11:Remove 1 and add in array.
Output: Sorted array 1,2,3,4,5
public class heap_Sort{
public static void main(String a[]){
int i;
int arr[] = {1,3,4,5,2};
System.out.println("\n Heap Sort\n---------------\n");
System.out.println("\n Unsorted Array\n\n");
for (i = 0; i < arr.length; i++)
System.out.print(" "+arr[i]);
for(i=arr.length; i>1; i--){
fnSortHeap(arr, i - 1);
}
System.out.println("\n Sorted array\n---------------\n");
for (i = 0; i < arr.length; i++)
System.out.print(" "+arr[i]);
}
public static void fnSortHeap(int array[], int arr_ubound){
int i, o;
int lChild, rChild, mChild, root, temp;
root = (arr_ubound-1)/2;
for(o = root; o >= 0; o--){
for(i=root;i>=0;i--){
lChild = (2*i)+1;
rChild = (2*i)+2;
if((lChild <= arr_ubound) && (rChild <= arr_ubound)){
if(array[rChild] >= array[lChild])
mChild = rChild;
else
mChild = lChild;
}
else{
if(rChild > arr_ubound)
mChild = lChild;
else
mChild = rChild;
}
if(array[i] < array[mChild]){
temp = array[i];
array[i] = array[mChild];
array[mChild] = temp;
}
}
}
temp = array[0];
array[0] = array[arr_ubound];
array[arr_ubound] = temp;
return;
}
} Notes: This isn't an especially useful sort, but the running time is guaranteed O(n.log n) and it is very light on memory consumption. Also, if you have already implemented a heap for some other reason, then this sort comes almost for free. It is possible to get some extra speed by constructing the heap in one pass: put everything into the heap ignoring the heap condition, then work through the heap from bottom to top, bubbling elements down the heap where necessary. This makes the heap creation take linear time.
Reference: roseindia
No comments:
Post a Comment